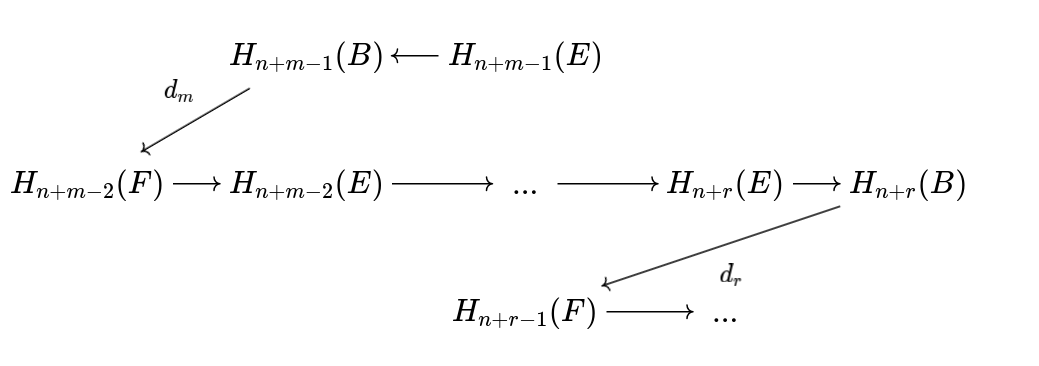
Apprendre à vivre enfin. - J.D.
27/01/2026
The homotopy groups of a space, X, along with the the set π0 is a left-exact functor, in the sense that it carries fibre-sequences to long-exact sequences of homotopy groups. Of course, this is modulo appropriate additional qualifiers "on the fringes", π1 and π2. On the other hand, integral homology is right-exact: it carries co-fibre sequences to long-exact-sequences of homology groups- In fact, this is true of all generalised homology theories.
The failure of π to be right-exact and of H to be left-exact is a trace of the general non-stability of the homotopy category of spaces. As it turns out, the connectivity of a space is a measure of the "stability" of its homotopy type. This is reinforced by observation that an n-connective space, X, is equivalent to its n-fold loop space ΩnX equipped with the structure of an n-fold loop space. The heuristic here is that n-fold spaces reflect the stability of the n-sphere, which of course goes to infinity as n does.
We can make our claim very precise. The most common such proposition Freudenthal Suspension Theorem. However, the Freudenthal theorem and its relatives can be viewed as corollaries of the general theory of transgression, which stems from the following elementary observation.
Proposition Let F→E→B be a fibre sequence, where B is m-connected and F is n-connected, and suppose that m,n>0. Then, for n< m, there exist trangression maps dr:Hn+r(B)→Hn+r-1(E) sitting in a long-exact-sequence.
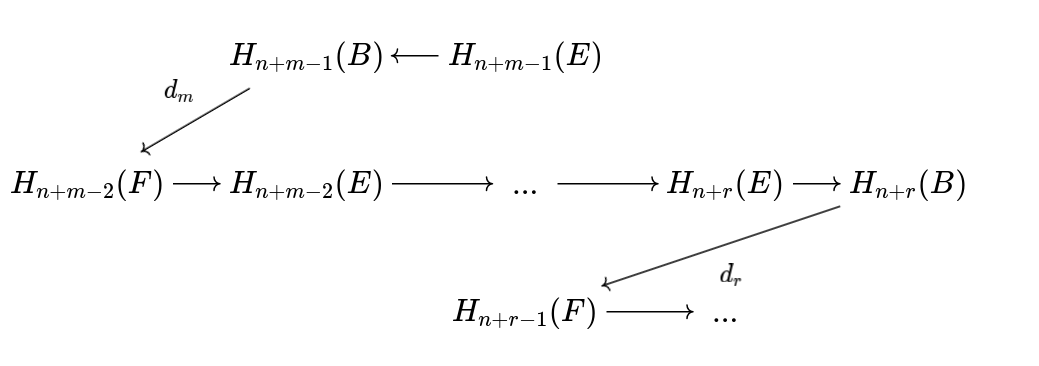
The existence of these maps is not interesting in and of itself: I haven't told you how to extract them yet. In any case, they are not lying any deeper than the Serre spectral-sequence of homology. However, inspecting this spectral sequence closely, one see that (i) the transgression maps are natural in the fibration and (ii) they commute with the boundary map in the long-exact-sequence of homotopy groups. That is to say, for r< m, the following diagram commutes:
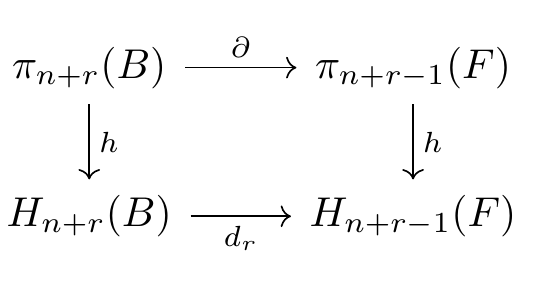
23/01/2026
n-Connected spaces admit reduced models . More precisely, pointed, n-connected Kan complex admits a strong deformation retract onto a subcomplex which has single cell in each level less than n. This type of construction factors into Quillen's thoery of minimal models , which in turn allows one to establish the equivalence between simplicial homotopy theory and the homotopy theory of topological spaces.
Among the immediate corollaries of "n-reduction" is the classical theorem of Hurewicz.
Theorem: X a pointed space. h:π(X)→H(X) is the Hurewicz map.
(1) The Hurewicz map π0:→H0(X, pt.) is the free Abelian group on π0.
(2) The Hurewicz map h:π1(X)→H1(X) is the Abelianisation of π1(X).
(3) If X is n-connected, for n>0, then the Hurewicz map is an isomorphism in degrees less than n+1 and an epimorphism in degree n+2.
Edited 25/01/2026